MIHAILO PETROVIĆ ALAS’S HYDRO INTEGRATOR
Radomir S. Stanković
THE HYDRO INTEGRATOR MADE BY MIHAilo Petrović Alas is the first analogue computing machine operating according to the principle of capillary flow of fluids. Petrović’s work on this machine was announced in 1896 by Professor of Mechanics at the Grand School in Belgrade, Ljubomir Klerić. The first paper on the topic of hydraulic integration Petrović published in 1897 in Comptes rendus de l’Académie des Sciences de Paris, and its Serbian translation with additional explanation of certain details appeared in 1898 in Srpski tehnički list (Serbian Technical Journal), the journal of the association of Serbian engineers and architects. He published on this topic again the same year, in the French language, in American Journal of Mathematics. A perfected version, which is considered to be the highest development of the hydro integrator, was described in the same Journal a year later. The work on the hydro integrator can be considered a result of research which Petrović called materialization of mathematics ensuing from studies of mathematical phenomenology. Mathematical phenomenology was one of several academic disciplines Petrović intensely engaged in. According to Petrović, the central stage in this academic branch is occupied by establishment of analogies between physically often disparate phenomena and their reduction to the same abstract essence, the so-called phenomenological type of fact. By introducing mathematical apparatus, Petrović has shown that certain mathematical problems can be solved in this way.

Figure 1 Petrović’s sketch of a hydro integrator (Digital Legacy of Mihailo Petrović Alas)
Materialization of analytical (mathematical) problems for Petrović implied that one should find for a given problem some concrete physical phenomenon for which the same relations and the same laws hold, and which would be then resolved by analysis of the observed, related, problem and phenomenon. From this point of view, the hydro integrator made by Mihailo Petrović was based on an analogy between properties of solution of certain classes of differential equations and behavior of fluids when a body is dipped into a vessel filled with fluid.
Figure 2 shows a 3D model of a hydro integrator. The author of the 3D model shown in Figures 2 and 4 is Petar Vranić of the SASA Mathematical Institute.
The Hydro Integrator’s Construction
The hydro integrator made by Mihailo Petrović consists of two fundamental entities – the arithmetic device and the input-output unit.
The arithmetical devise consists of a vessel of a certain shape filled with fluid, body also of a precisely defined shape, and a float.
The input unit is made up of a body of a certain shape with or without the rotating cylinder. In the first variant, input data are represented by the function of a body shape. In the second variant, these are the function of a body shape and the function determined by its graph on the input rotating cylinder.

Figure 2 3D model of the hydro integrator, the author of the 3D model Petar Vranić (Mathematical Institute of SASA, Belgrade)
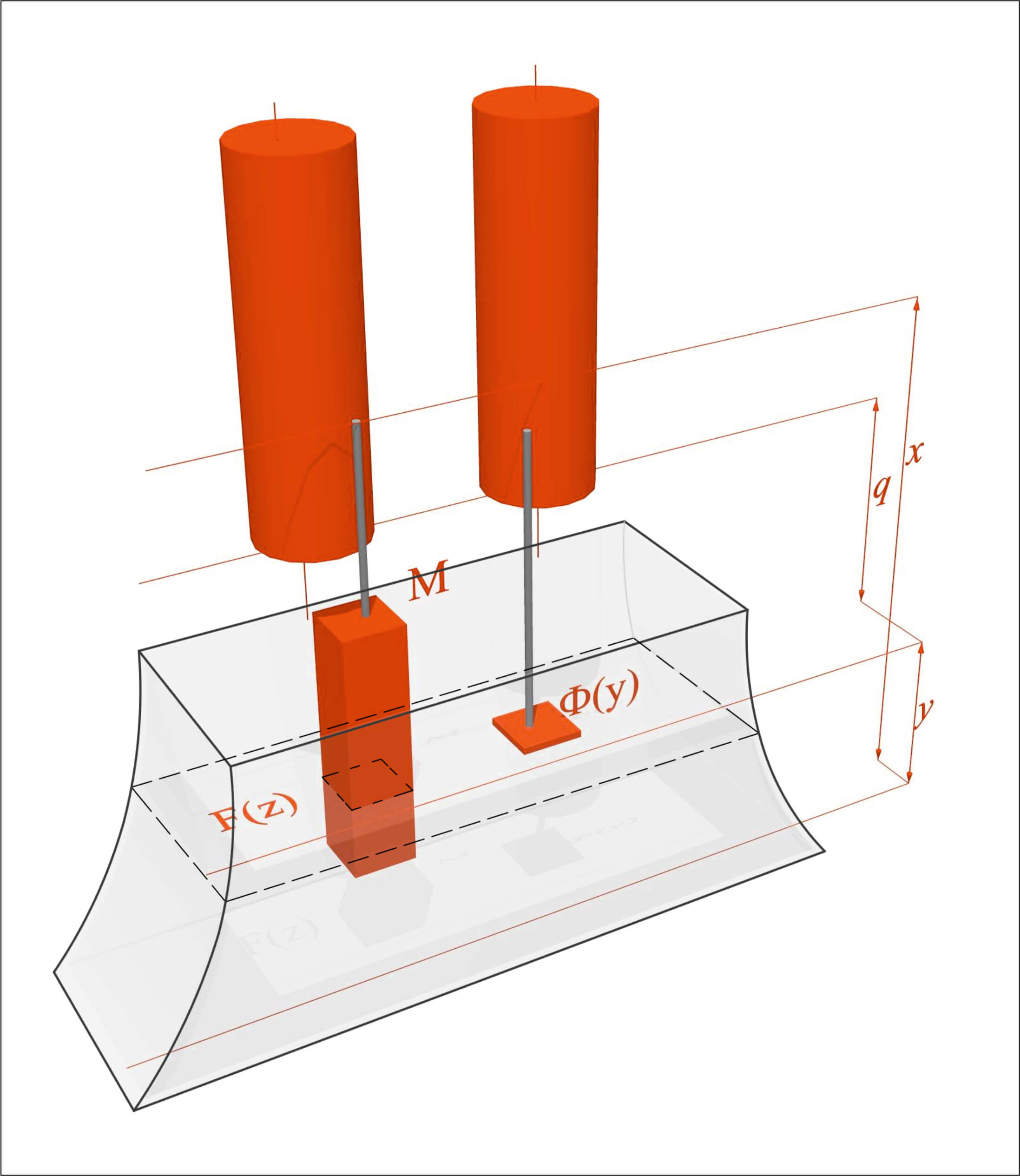
Figure 4 Illustration of the principle by which the device works, the author of the 3D model Petar Vranić (Mathematical Institute of SASA, Belgrade)
The output unit consists of one or several rotating cylinders connected with the float in the arithmetic device. On the cylinders, the solutions of equations are drawn in the form of functions, which as a technical solution was proposed already in the 1897 paper. The idea about that occurred to Petrović in 1892 during lectures of professor Königs who was teaching at Collège de France in Paris. This can be corroborated by a sketch of the cylinder as a part for writing down solutions obtained by applying a device, found in a notebook from these lectures, shown in Figure 3.

Figure 3 Petrović’s sketch of the rotating cylinder as an element of a hydro integrator (Library of SASA, А40/120)
The final version of the integrator uses a clock mechanism with permanent angular velocity in order to harmonize the work of the input and output cylinders which are connected kinematically. This enables that the data on the input cylinder should cross an equal distance in the same time. Owing to that, the device can be considered a combination of a machine of a kinematic and of a hydraulic type which for the developed input mechanism solves one specific differential equation. In Figures 1 and 2, it can be seen that the construction of the hydro integrator enables the vessel with the fluid, and the body being dipped in it, to be added on the exterior side of the device, so that their replacement is simple. Therefore the same device with the choice of the vessel and the body of various shapes can be used for solving several equations.
The principle of work of the hydro integrator
The principle of work of the hydro integrator is depicted in Figure 4 and is based on the following consideration.
What determines the alteration of the level of the fluid in vessel $B$ due to the dippling of a body $M$ in it is the shape of both body $M$ and the vessel $B$. If $Ф(y)$ and $F(z)$ are the surfaces of the horizontal intersection in the same plane of vessel $B$ and body $M$, then the factor $x$ related to the position of the body when being dipped changes into $x−dx$, while the level of fluid rises from y to $y+dy$, which makes volume of fluids which had shifted from $y$ to $y + dy$ equal $(\Phi(y) − F(z))dy$. Given that the volume of the fluid squeezed out is equal to the volume of fluid which is occupied by the body $M$ dipped for the factor of $z$, that is, $F(z)dz$, consequently we have
\begin{eqnarray*}
(\Phi(y) – F(z))dy = F(z)dz,
\end{eqnarray*}
or expressed differently, when the relation $z = x − y$, holds, then
\begin{eqnarray*}
\frac{dy}{dx}=\frac{F(x-y)}{\Phi(y)}.
\end{eqnarray*}
By choice of various intersections of the body M and the vessel B, the hydro integrator can be used for solving a broader class of differential equations. As Petrović had said, each manner of realization of the hydro integrator corresponds to entire classes of the first-order differential equations that can be integrated with it, and the entire classes of curves that can be continually constructed.
From the point of view of contemporary computers, the pair (body, vessel) corresponds to sub-programs the choice of which can perform integrating of the broader class of equations. By choosing the input data, one obtains a list or a library of equations that can be solved in this way. The hydro integrator, the way it was initially proposed by Mihailo Petrović, could solve two classes of differential equations.
$$P(x,y)dx + Q(x,y)dy.$$
Petrović stated the same device could solve both classes of equations by changing the vessel and the shape of the body being dipped by applying several vessels and integral cylinders, which was the reason for the construction that is shown on Figure 1 with the aim to enable the simple replacement of the vessel and the body as the basic elements of the arithmetic unit of the device.
\begin{eqnarray*}
\frac{dy}{dx}=X(t) – \lambda^2y^2
\end{eqnarray*}
The class (1) contains the Riccati’s equation as well as some other types of equations.
Let us be reminded that for example, Jacob’s integrator could solve only the first-order Riccati’s equation, so the advantages of the solution proposed by Petrović can clearly be seen.
The scientific-academic promotion of the hydro integrator
The hydro integrator made by Mihailo Petrović was shown at the World Exhibition in Paris in 1900 in the Pavilion of Serbia, designed by architect Milan Kapetanović, a professor of descriptive geometry at the Technical Faculty of the Belgrade’s Grand School. At this exhibition the hydro integrator made by Mihailo Petrović was awarded by the gold medal. The device was constructed by a French specialist in precise mechanisms whose name has not been recorded, although the information about the contracting of a craftsman is contained in the letter which Mihailo Petrović had sent to the Minister of National Economy, in which he pleaded financial support for the construction of the device, equaling one thousand and five hundred dinars at the time.
The device exhibited at the World Exhibition had full functionality and its operation was shown to the visitors of the exhibition. It is considered to be the most fully executed example of the hydro integrator ever built. The reconstruction of the device was done by Professor Dragan Trifunović in 1980, and its physical realization was carried out with the assistance of the architect Gradimir Bosnić. This reconstruction is situated in the Mathematical Office of the Faculty of Forestry in Belgrade. Considering that during the World Exhibition in Paris the International Congress of Mathematicians was being held in Paris from August 6 to August 12, 1990, the participants could inform themselves about this way of solving differential equations, and be assured about the records of its success and accuracy. This was concurrently the first congress of mathematicians in the work of which Mihailo Petrović took part.
The contribution of Mihailo Petrović
The original contribution of Petrović to world science in the field of devices for solving analytical problems is the hydro-dynamic model for solving various classes of differential equations, which was already the topic of his first description of a hydro integrator in the Serbian Technical Journal-Srpski tehnički list in 1898. Subsequently, special contribution is made by the application of elements of calculation regarding the shape of the body dipped into water. Furthermore, it is important to mention also the combination of the hydraulic principle and the kinematic connection in the final version of the hydro integrator.
Petrović also talks about the connection between analytical facts associated with line integrals and geometrical facts from the theory of minimal surface with capillary action. The idea is that a hydro integrator can consist of several vessels in the arithmetic device that would be equipped with capillary tubes. Such a solution was later used in the hydro integrator from 1936 proposed by Lukyanov, for solving Fourier’s partial differential equation in accordance with the principle of analogy between thermal conductivity and the model of circulation of fluid in capillary tubes.
The work on the hydro integrator is among the most-often cited mathematical accomplishments of Mihailo Petrović. It is considered to be the first device for solving differential equations in accordance with hydraulic principles, and to facilitate solving a broader class of equations. In addition to the gold medal awarded in Paris, this invention was honored with other international awards. Petrović was thus in 1907 awarded with the honorary diploma of the London Mathematical Society.