ACADEMIC ACHIEVEMENTS

Stevan Pilipović

Some of the most important results Petrović obtained were already in his doctoral dissertation, therefore we will describe in short the topic of this dissertation and its main result. In his thesis, Petrović studied a class of non-linear first order differential equations, as well as a class of non-linear second order differential equations; the latter are well-known as Painlevé equations. This topic was very popular at the time. In the late 19th century, the most well-known names in French and world mathematics, Picard, Painlevé and Fuchs, studied non-linear second-order equations with no movable branch points. In that context, Painlevé, later Fuchs, and even later (1910) Gambier described the sub-class of these equations which take the following form:

$y”=F(x,y,y’)$

whereby $F$ is the quotient of two polynomials with respect to $y$ and $y’$ with holomorphic functions as coefficients. Painlevé has found fifty general forms which have immovable branch points which he, with the assistance of Fuchs and Gambier, reduced to six essentially new equations. These are the equations that cannot be solved in terms of familiar special functions such as elliptic functions, those that cannot be solved in terms of linear equations and that also cannot be transformed from one into the other. These six equations bear the name Painlevé transcendents. These six generic cases today have a great significance in many areas of analysis, algebra and geometry, but also in applications such as statistical mechanics, physics of plasmas, non-linear wave theory, quantum gravity theory, quantum field theory, theory of relativity and nonlinear optics. Painlevé obtained his first results in papers published in 1887 and 1895. This problem had also been addressed by the other greatest mathematicians of that time, Poincaré and Picard. We particularly emphasize this fact, considering that Mihailo Petrović had defended his doctoral disseration in front of a commission consisting precisely of Picard and Painlevé.

The front cover and the first page of Petrović’s doctoral thesis (University Library “Svetozar Marković”)

The doctoral dissertation of Mihailo Petrović is dedicated to the immovability of zeros, poles and essential singularities in solutions of algebraic first– and second-order differential equations. In accordance with the definition, singularities of solution consist of their poles, essential singularities, final and logarithmic branch points, while movability is defined as a property according to which zeros and singularities are constantly changing as initial conditions of a given equations change. In other words, the property of movability determines whether a problem behaves “well,” unlike the problem which behaves “badly” and which often does not have a solution if initial conditions change. Mihailo Petrović studied problems for which solutions of equations often have singularities independent of the change of initial conditions.

In this first part of his doctoral dissertation, Mihailo Petrović analyzes first-order equations in which one has products of powers of an unknown function y, powers of its derivative $y’$, and of holomorphic functions with respect to the independent variable $x$:

\begin{eqnarray*}
F(x,y,y’) \equiv \sum_{i=1}^{s} \phi_{i}(x)y^{m_{i}}(y’)^{n_{i}}=0.
\end{eqnarray*}

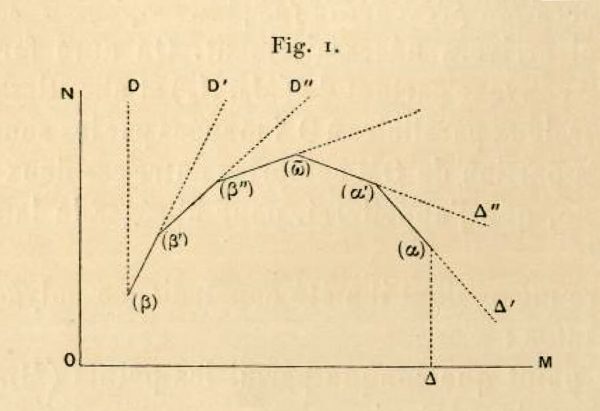
In the statement of the main result of his thesis, an important role is played by a polygon $P$ which Petrović constructs in the following way. Polygon $P$ has an $s$ vertices $(M_{i},N_{i})$, $N_{i} =n_{i}$, $M_{i} =m_{i} + n_{i}$ , $i= 1, \ldots , s$, which have been done according to certain rules, while it designates with $(M_{\alpha},N_{\alpha})$, that is, $(M_{\beta},N_{\beta})$, the most distant i.e. the most proximate vertices to the axis ΟΝ, while λ designates coefficients of the direction of the sides of the polygon. His results subsequently is: Poles and essential singularities of the general solution of the first-order equation $F(x,y,y’)=0$ do not change with the constant of integration if and only if the adjacent polygon does not have any vertex right of the highest elevated vertex of the polygon. For the existence of a movable zero of an $\lambda$  order, it is necessarz and sufficient for the polygon to have a side with an $\lambda$ inclination and to have the moveable pole of an $\lambda$  order, if and only if the polygon has a side with an inclination $-\lambda$.

According to the data analyzed by the historian Dr. Dragan Trifunović, Petrović published 393 papers of which 328 are mathematical manuscripts from twelve different areas in the most prominent journals of that time, as well as today. In academic journal Comtes Rendus, in which, in the opinion of French mathematicians, the very best papers appear, Mihailo Petrović published as much as thirty papers. He has also published his work in Acta mathematica, Mathematische Annalen (two papers), Bulletin de la Sociètè mathèematique de France (fourteen papers), American Journal of Mathematics (three papers), as well as in numerous other Swiss, German, Czech and Polish journals. In terms of the number of published manuscripts in leading international journals, Petrović is still one of the most productive Serbian mathematicians of all times.

Petrović’s first paper anticipated the topic of his doctoral dissertation and the papers which followed subsequently build up on the results from his dissertation. Independence with respect to constants, of singularities, zeros, extremes and some other properties of a general solution dominates in all these papers as the clear determinant of Petrović’s academic work. This property is the essential, constitutive characteristic of the model he is studying, that is, the equation that describes this model. When he describes the residuum of function, studies the so-called binomial equations of the first order, the asymptotics of the solution, writes about “one class of second-order differential equations” or the nature of the solution, to paraphrase titles of some of his papers, internal structural relation between the dependent and the independent variable depicted by the very equation remains the central goal of his explorations. A great creative potential in academic work, displayed in his doctoral dissertation, is also visible in papers written and published in the period of the First World War when Picard, Appel and Hadamard were publishing them in Comtes Rendus. During the First World War, he resided in Switzerland, where he worked as a cryptographer of the Serbian Army Command. Despite this engagement, he has had sufficient energy to also delve in serious mathematical problems.

A quantitative analysis of solutions of differential equations, without solving the equation itself, as well as solving certain classes of equations, represent a significant part of the mathematical opus of Mihailo Petrović. In time, as he started to spend more and more time in Serbia and less and less time at the Sorbonne, we can notice that Petrović was engrafting new ideas on the ideas from his doctoral dissertation, as well as on his extraordinary knowledge of the theory of analytical functions. In most of his initial papers from the late 19th and early 20th century, he mostly elaborated the ideas he has developed during his residence and his scholarly work in France. Naturally, the advantages of residing in France had been great and numerous. There, Petrović had access to the latest and crucial literature, and in addition he had immediate contacts with the greatest mathematicians of that time, with whom he could exchange his ideas and results and discuss them. Considering that in his thesis he particularly studied solutions of the equation $y’= R(t,y)$ with the Painlevé property, he explored in particular various forms of Riccati’s equation

$z'(t) = 2α(t)z(t) + b(t) -c(t)z^2(t),$

which can be solved with integrations and familiar special functions. Fuchs has shown that first-order equations, which were also studied by Petrović and solutions of which contain immovable branch points, boil down to matrix form of the Ricotta equation. Several dissertations by his doctoral students used this fact as a starting point. Petrović’s mathematical achievements are not exhausted with and do not rely exclusively on aforementioned ideas and methods. To him, but also to his doctoral students, comparison theorems for solutions of equations with respect to comparison of coefficients or right-hand side of equations, the so-called Sturm type theorems frequently provided an inspiration. His research often features simple but fine mathematical witticism with which he managed to obtain results of a general character for various classes of linear and nonlinear equations. Asymptotics of the solution, mostly of nonlinear Riccati-type equations, has also occupied an important place in his analysis of equations.

Petrović’s papers belong primarily to the following areas of analysis: differential equations, complex and real analysis. In numerical mathematics, he has given an important contribution, a monograph An Analysis of Number Intervals. With this monograph, interval numerical analysis has received an stimulus. At the very beginning of the 20th century, in the era of analytic theory of functions, Petrović studied functions the Taylor series of which do not have zeros in appropriate circle of convergence. Renowned mathematicians Landau, Hardy Fejér, Montel, Pólya, were very interested and have studied the solutions Petrović had obtained in this field, while German mathematician Jentsch has elaborated these results further in his doctoral dissertation. The well-known Petrović’s inequality is the result associated with convex functions. It served as an inspiration to several of his pupils to study inequalities and to achieve significant success in this area. The textbook monograph Elliptic Functions is even today a favorite read in this important area of analysis. This does not exhaust the range of Petrović’s mathematical interests. For example, in several papers he engaged in determining – computing integrals with the use of series.

Petrović also produced work in the field of algebraic equations. In this area, particularly interesting is his work on geometry of zeros of a polynomial, which was also studied by the said group of famous mathematicians Landau, Hardy Fejér, Montel, Pólya. He determined a circle in which an algebraic equation has at least one root without using Rouché’s theorem. His paper from 1899, published in Comtes Rendus, is the first paper which determines the number of zeros contained in the given circle.

Reading academic papers by Mihailo Petrović in the period after the Great War, a gradual decline in quality is noticeable. Papers are less deep, but still bear certain ideas that have perhaps been already propounded, but which are nevertheless instilled with new energy. Contrary to contemporary style, Mihailo Petrović exhibits his results going from the specific towards the general. He had an ease of writing and in his manuscripts, as in a tale, he would first expound simple conclusions which he would gradually generalize and finally fully explain and transform into axioms. Such an approach has enabled a reader to easily follow his argument and understand the goals of the manuscript from its starting point.

Among his academic achievements, the monograph Mathematical Specters (which is not related to contemporary, very developed, spectral theory of operators) in which Petrović, analogous to the light spectrums, develops a theory of mathematical specters. This very comprehensive, voluminous and original work by Petrović does not belong to analysis, but is closer to theory of numbers and cryptography, the disciplines he also showed an interest in. The basic idea of this theory of his is to code infinite series of data with infinite decimal developments of real numbers and then to translate mathematical operations with data into certain numerical or combinatory procedures with numbers – their codes. Petrović was particularly interested in repetitions in groups of numbers and he has seen an analogy in that with physical spectrums. Even though he had written the book in French, had received praise by some French mathematicians, and held one semester of lectures at the Sorbonne, this theory nevertheless did not significantly take root. An interesting view on it is expressed by French mathematician Bul, who in his review of this work at one point says that “such analogies are risky and like arches of the shiniest rainbow can be very seductive, but also illusionary.” On the other hand, contemporary digital computers, as implied by their very name, do not do anything else but precisely employ elementary arithmetical and basic combinatory operations over binary codes of series of data, even though the semantics of our problem concerning data and the resolving algorithm is found at some utterly different place. Therefore we can consider this work by Petrović as simply a work that appeared ahead of its time. His student, professor Konstantin Orlov, one of the most prominent heirs of professor Petrović in the field of differential equations and numerical analysis, has dedicated some attention to this area in his dissertation.

The contributions which pertain to application of differential equations, given in his famous work Phenomenology, as well as in a series of papers describing models in physics and chemistry, are portrayed in separate texts in this Catalogue.

Mihailo Petrović was rather a ‘loner’ as a scholar. All papers, except one together with Karamata, he authored alone. The sole collaboration is interesting because it corrects one mistake made by Poincaré. The reason for this is his extreme individuality. He did not always elaborate ideas to the end, so that others, taking into account his results and ideas, have written more profound papers which, among other things, have also been more often quoted. Among colleagues, there were none who particularly promoted him also due to the fact that all of them, and here I refer to mathematicians in France, primarily sought after and were primarily aspiring to personal prestige, despite Petrović’s generous nature and propensity to form genial friendships. Given that at the time there were few mathematicians in Serbia and that Petrović was our first mathematician who addressed these problems, he could not experience significant mathematical support in Serbia, especially in the period between the two World Wars.

Mihailo Petrović was not very interested in being referenced by other authors and it did not interest him whether other mathematicians read his work or not. On the other hand, mathematicians at the end of the 19th and the beginning of the 20th century did not have many possibilities for quoting other authors, and did not have the habit of such mutual academic behavior. In the dissertation of Mihailo Petrović, as well as in his other papers, quoting of results of other mathematicians does not appear in the form which is generally established today. In the field in which Petrović worked, citiations most often referred to results of Picard, Fuchs and certainly unparalleled, Painlevé. Mihailo Petrović himself in his dissertation has quoted very few sources, giving only eight references. The papers by Mihailo Petrović were quoted at the time close to the period in which he wrote them, but we think it was too insufficient. The papers in Acta Mathematica, Mathematical Annals (Matematički anali) and a series of other journals, dedicated to the problematics addressed in his doctoral dissertation, as well as most other papers, were quoted in late 19th and early 20th century. The results of Petrović’s first paper published in Comtes Rendus are cited in full in the famous and most highly acclaimed monographic book by Picard at the time, while the results of the doctoral dissertation are cited in Encyclopedia of Mathematics. However, in the vortex of events of the Balkan wars and the First World War, Mihailo Petrović slowly became less and less present in France, which also meant in world circles in which new science was created and developed.

Mihailo Petrović presented his work at a series of important international congresses of mathematics in Paris, Rome, Cambridge, Toronto and a conference of academic federations of France (a dozen times), Romania, Italy, Slavic countries and Balkan countries.

Petrović was appreciated and valued-esteemed as a scientist not only in Serbia but also in all of Europe. He was a member of Yugoslav Academy of Sciences and Arts, Czech Royal Academy, Polish Academy of Sciences in Krakow, Academy of Sciences in Warsaw, Romanian Academy of Sciences and a whole series of mathematical societies in Paris, Palermo, Bucharest, Leipzig, Prague, Lviv and in Paris he was a member of several scientific societies and academic associations.

His contribution in the area of teaching and education

Acting in the role he assumed due to fortunate circumstance, academician Petrović was of first-rate importance for the development of university teaching of mathematics in Serbia. In the period up to the First World War, as well as in the inter-war period, Professor Petrović was developing, almost alone, the university system of mathematical education of Serbia. He was a full professor of mathematics since 1894 at the Grand School at the Faculty of Philosophy and since 1905 at the University of Belgrade. He was the only one who supervised mathematical PhDs at the University of Belgrade from 1912 to 1941. He did not publish a lot of textbooks, only three, but his hand-written manuscripts are of extraordinary quality and a genuine pleasure to read even today. He held as much as 16 different courses: 10 courses in analysis and differential equations, 2 courses in algebra, 3 courses in numerical mathematics and a special course in phenomenology. He wrote eight manuscripts. He was a member of the commission for taking the professorship exam, was an envoy of the Ministry for the maturity exams, the president of the Supreme Educational Council of Serbia, a reviewer of high-school textbooks and published several papers dedicated to teaching methods.

Mathematical offspring of Professor Petrović: academician Slobodan Aljančić (Archive of the Mathematical Institute of SASA (MISASA)), academician Bogoljub Stanković (author: Dragan Aćimović, 2016) and professor Slaviša Prešić (author: Dragi Radojević, 2006)

Mihailo Petrović was a strict and principled professor. It has been noted that he held not a single public speech, although this is not unusual for a mathematician. With Milutin Milanković and Anton Bilimović in 1932, he established a journal entitled Publications de l’Institut Mathématique. The results of a greater engagement in his teaching work remains unknown for many of our mathematicians, who are mathematical heirs of Professor Petrović. A great number of mathematicians in Serbia have Mihailo Petrović Alas as their mathematical predecessor. In addition to students of academician Đura Kurepa and Serbian mathematicians who graduated abroad under the supervision of various professors, as well as geometricians whose predecessor was Danilo Blanuša, a great number among us have Mihailo Petrović as their close mathematical ancestor. Let us enumerate the names of his students of the first generation: professors Miroslav Berić, Sima Marković, Dragoljub Mitrinović, Konstantin Orlov, Tadija Pejović, Danilo Mihnjević, Miloš Radojčić. Among the first generation are also academicians Radivoj Kašanin and Jovan Karamata, and academicians among the second generation are Vojislav Avakumović, Miodrag Tomić, Slobodan Aljančić, Vojislav Marić, Milosav Marjanović, Dragoš Cvetković, Gradimir Milovanović, and among the third generation members of the Academy include Ivan Gutman, the correspondent member Miodrag Mateljević and the author of this article.

I feel greatly obliged to acknowledge our very renowned deceased mathamaticians who are descendents of academician Petrović, namely professors Manojlo Marović, Ernest Stipanić, Tatomir Anđelić, Milorad Bertolino, Milica Dajović and Vojin Dajović, Petar Vasić, Slaviša Prešič, Milivoj Lazić, Zagorka Šnajder, Svetozar Milić, Zoran Ivković, Janez Ušan, Dušan Adamović, Dragoljub Aranđelović, Vladeta Vučković, Bogdan Bajšanski, Ranko Vojanić, Tatjana Ostrogorski, Zoran Popstojanović, Ljuba Protić, Rade Dacić… All of them are have had a connection with academician Mihailo Petrović. Many names have not been mentioned. The information about them, as well as about those who are still active, can be found in the mathematical genealogy of academician Petrović, which is a part of this Catalogue.

His work in the Academy of Sciences and Arts

Jovan Karamata was promoted to an Academy member in 1939. To his teacher, Mihailo Petrović, he provided great assistance in systematizing academic publications. It is owing to him and to the great desire of Mihailo Petrović to catalogue his papers and his legacy that today we have a comparitive wealth of data about his life and work.