Хидроинтегратор Михаила Петровићa Аласа
Радомир С. Станковић
Хидроинтегратор Михаила Петровића Аласа је прва аналогна рачунска машина која ради на принципу кретања течности. Петровићев рад на овом уређају најавио је још 1896. професор механике на Великој школи у Београду Љубомир Клерић. Први рад на тему хидрауличне интеграције Петровић је објавио 1897. у Comptes rendus de l’Académie des Sciences de Paris, а његов превод на српски језик уз додатно објашњење одређених детаља 1898. у Српском техничком листу, који је био орган удружења српских инжењера и архитеката. Наредну публикацију на ову тему објавио је на француском језику исте године у American Journal of Mathematics. Усавршена верзија, која се сматра завршним решењем хидроинтегратора, описана је у истом часопису наредне године. Рад на хидроинтегратору може се сматрати резултатом истраживања које Петровић назива материјализацијом математике произашлим из проучавања математичке феноменологије. Математичка феноменологија била је једна од више научних дисциплина којима се Петровић интензивно бавио. Према Петровићу, главно место у овој науци има успостављање аналогија између физички често диспаратних феномена и њихово свођење на исту апстрактну суштину, тзв. феноменолошки тип факата. Увођењем математичког апарата Петровић показује како се на овај начин могу решити поједини математички проблеми.

Слика 1. Петровићева скица хидроинтегратора.
Под материјализацијом аналитичких (математичких) проблема Петровић подразумева да се за дати проблем пронађе конкретна физичка појава за коју важе исте релације и исти закони који би се добили аналитичким решењем посматраног проблема. Са овог становишта, хидроинтегратор Михаила Петровића заснован је на аналогији између особина решења одређених класа диференцијалних једначина и понашања течности приликом урањања неког тела у суд са течношћу.
На слици 2 приказан је 3D модел хидроинтегратора. Аутор 3D модела представљеним на сликама 2 и 4 је Петар Вранић из Математичког института САНУ.
Конструкција хидроинтегратора
Хидроинтегратор Михаила Петровића се састоји од две основне целине– аритметичког уређаја и улазно-излазне јединице.
Аритметички уређај чине суд одређеног облика напуњен течношћу, тело такође тачно дефинисаног облика и пловак.
Улазну јединицу чини покретно тело одређеног облика са или без ротирајућег ваљка. У првој варијанти, улазни подаци представљени су функцијом облика тела. У другој, то су функција облика тела и једна функција задата својим графиком на улазном ротирајућем ваљку.

Слика 2. 3D модел хидроинтегратора.
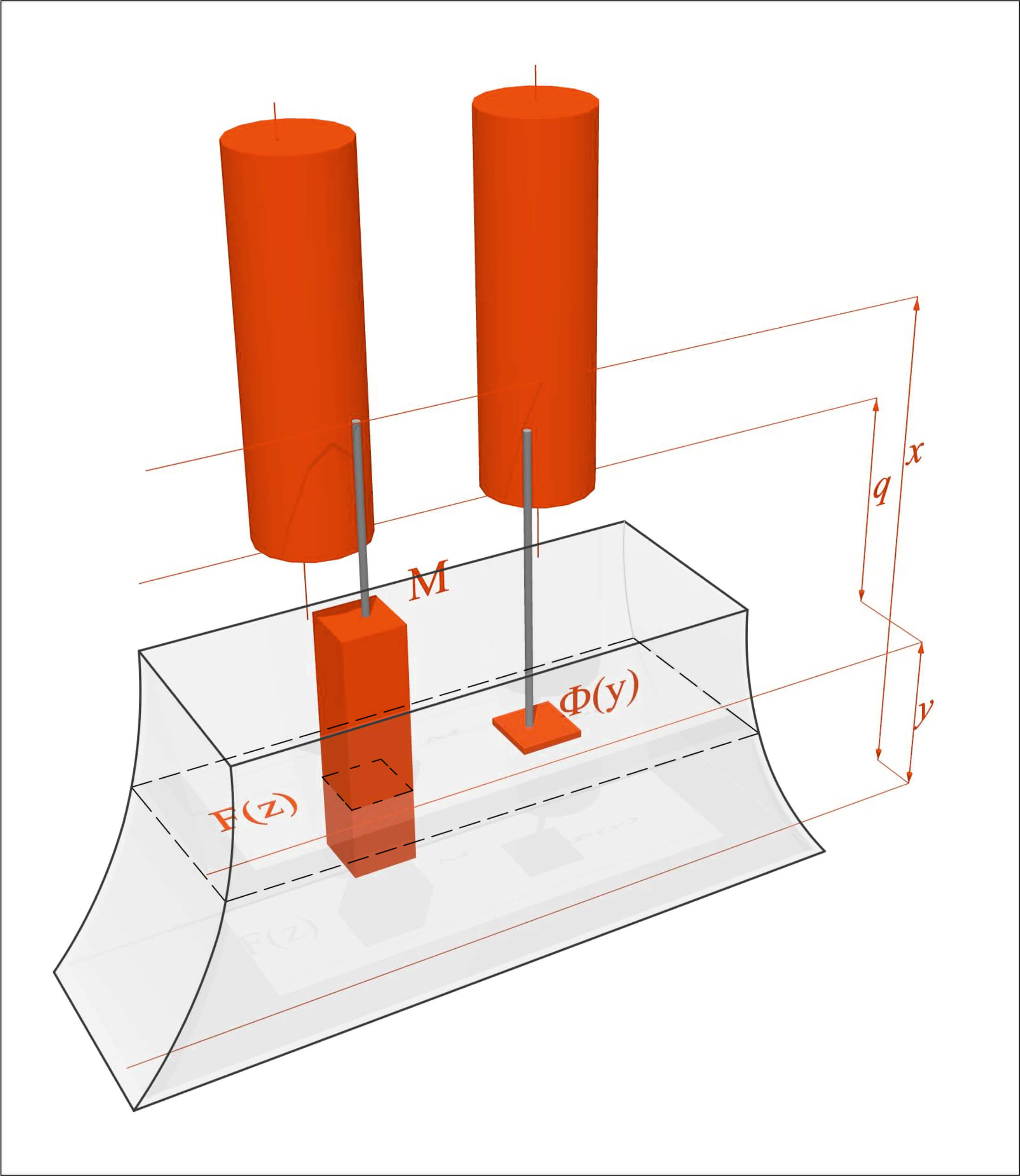
Слика 4 Илустрација принципа рада уређаја
Излазна јединица се састоји од једног или више ротирајућих ваљака повезаних са пловком у аритметичком уређају на којима се исцртавају решења једначина у облику функција, што се као техничко решење предлаже још у првом раду из 1897. Идеју о томе Петровић је добио 1892. на предавањима професора Кönigs-а са Collège de France у Паризу. О томе сведочи скица ваљка као дела за записивање решења добијеног применом неког уређаја у свесци са ових предавања приказана на слици 3.

Слика 3. Петровићева скица ротирајућег ваљка као елемента хидроинтегратора.
У завршној верзији интегратора коришћен је сатни механизам са сталном угаоном брзином ради усклађивања рада улазног и излазног ваљка спојених кинематички. Тиме је омогућено да податак на улазном ваљку за исто време прелази једнако растојање. Захваљујући томе уређај се може сматрати комбинацијом машина кинематичке и хидрауличне врсте која за изабрани улазни механизам решава једну одређену диференцијалну једначину. Према сликама 1 и 2, види се да конструкција хидроинтегратора омогућава да се суд са течношћу и тело које се у њега потапа додају са спољне стране уређаја, тако да је њихова замена једноставна. Отуда се исти уређај избором суда и тела различитих облика може користити за решавање више једначина.
Принцип рада хидроинтегратора
Принцип рада хидроинтегратора илустрован је на слици 4, а заснован је на следећем разматрању.
Промена нивоа течности у суду $B$ услед потапања у њега тела $M$ одређена је обликом како тела $M$ тако и суда $B$. Уколико су $Ф(y)$ и $F(z)$ површине хоризонталног пресека у истој равни суда $B$ и тела $M$, тада се величина $x$ везана за положај тела приликом потапања мења у $x−dx$, док се ниво течности повећава од y на $y+dy$, што чини да је запремина течности која се померила са $y$ на $y + dy$ једнака $(\Phi(y) − F(z))dy$. Како је запремина истиснуте течности једнака запремини течности коју заузима тело $M$ уроњено за величину $z$, односно, $F(z)dz$, следује
\begin{eqnarray*}
(\Phi(y) – F(z))dy = F(z)dz,
\end{eqnarray*}
или написано на други начин, како је испуњена релација $z = x − y$, тада
\begin{eqnarray*}
\frac{dy}{dx}=\frac{F(x-y)}{\Phi(y)}.
\end{eqnarray*}
Избором различитих пресека тела М и суда B хидроинтегратор се може користити за решавање шире класе диференцијалних једначина. Како наводи Петровић, сваком начину реализовања хидроинтегратора одговарају читаве класе диференцијалних једначина првог реда које се њиме могу интегралити и читаве класе кривих које се могу континуално конструисати.
Са аспекта савремених рачунара, пар (тело, суд) одговара потпрограмима чијим избором може да се врши интеграљење шире класе једначина. Избором улазних података добија се листа или библиотека једначина које се могу на тај начин решавати. Хидроинтегратор, како га је иницијално предложио Михаило Петровић, могао је да решава две класе диференцијалних једначина, последње написану једначину и
$$P(x,y)dx + Q(x,y)dy.$$
Петровић наводи да би исти уређај могао да решава обе класе једначина променом облика суда и облика тела које се потапа уз примену више судова и интегралних ваљака, што је и био разлог за конструкцију каква је приказана на слици 1 са циљем омогућавања једноставне замене суда и тела као основних елемената аритметичке јединице уређаја. Класа (1) садржи Riccati-јеву једначину
\begin{eqnarray*}
\frac{dy}{dx}=X(t) – \lambda^2y^2
\end{eqnarray*}
као и неке друге типове једначина.
Подсетимо сe да је, на пример, Јаcоb-ов интегратор могао да решава само Riccati-јеву једначину првог реда, одакле произилазе предности решења које је предложио Петровић.
Научна промоција хидроинтегратора
Хидроинтегратор Михајла Петровића је приказан на Светској изложби у Паризу, 1900. године у Павиљону Србије који је пројектовао архитекта Милан Капетановић, професор нацртне геометрије на Техничком факултету Велике школе у Београду. На овој изложби хидроинтегратор Михаила Петровића био је награђен златном медаљом. Уређај је конструисао француски конструктор прецизних механизама чије име није остало забележено, мада се податак о ангажовању мајстора види из дописа Михаила Петровића министру народне привреде у којем тражи новчану подршку за изградњу уређаја у износу од хиљаду и пет стотина тадашњих динара.
Уређај изложен на Светској изложби је имао пуну функционалност и његов начин рада је био показиван посетиоцима изложбе. Сматра се да је то једини примерак хидроинтегратора који је био у потпуности изграђен. Реконструкцију уређаја је урадио професор Драган Трифуновић 1980. године, а физичку реализацију извео уз помоћ архитекте Градимира Боснића. Ова реконструкција налази се у Кабинету за математику Шумарског факултета у Београду. Како се за време Светске изложбе у Паризу одржавао Међународни конгрес математичара од 6. до 12. августа 1900. године, учесници су могли да се обавесте о овом начину решавања диференцијалних једначина и увере у његову успешност. Ово је уједно био први конгрес математичара у чијем раду је учествовао Михаило Петровић.
Доприноси Михаила Петровића
Оригинални допринос Петровића светској науци у подручју уређаја за решавање аналитичких проблема је хидродинамички модел за решавање различитих класа диференцијалних једначина, о чему се говори већ у првом опису хидроинтегратора у Српском техничком листу у 1898. години. Затим, посебан допринос представља примена калкулаторских елемената у облику тела зароњених у воду. Такође, значајно је поменути и комбинацију хидрауличког принципа и кинематичке везе у завршној верзији хидроинтегратора.
Петровић такође говори о вези између аналитичких факата везаних за криволинијске интеграле и геометријских факата из теорије минималних површина са капиларним појавама. Идеја је да хидроинтегратор може да се састоји од више судова у аритметичком уређају који би били снабдевени капиларним цевима. Овакво решење коришћено је знатно касније у хидроинтегратору из 1936. године који је предлагао Лукијанов за решавање Фоуријерове парцијалне диференцијалне једначине на принципу аналогије између топлотне проводљивости и модела кретања течности у капиларним цевима.
Рад на хидроинтегратору налази се међу највише навођеним математичким резултатима Михаила Петровића. Сматра се да је то први уређај за решавање диференцијалних једначина на принципу хидраулике, као и да омогућава решавање шире класе једначина. Поред освојене медаље у Паризу, овај проналазак доживео је и друга међународна признања. Тако је Петровић 1907. године награђен почасном дипломом Лондонског математичког друштва.