Научни резултати
Стеван Пилиповић

Слика 1. Михаило Петровић Алас.
После завршене Високе школе у Београду, Михаило Петровић је наставио студије математике и физике у Паризу и стекао дипломе „лисанс“ за математику и физику. Био је први инострани студент докторских студија из математике на Екол нормал супериjер, која је тада била, а и сада је, најчувенији образовни центар математике у свету. Петровићу су тамо предавали најпознатији математичари тог времена, између осталих Анри Поенкаре, Жан-Гастон Дарбу, Пол Апел, Пол Тенари, Шарл Ермит и Пол Пенлеве. У таквом окружењу главни пут ка успеху у математици били су таленат, оригиналност идеја и истрајност. Млади Михаило Петровић поседовао је и једно и друго и треће и био је један од најбољих студената генерације. Потврду томе дају и признања која је добијао као студент генерације. Одбранио је докторску дисертацију 1894. године а коментори су му били Ермит и Пикар. Петровић је у знак пажње тезу посветио Тенерију и Пенлевеу. Тако је ушао у свет великих математичара свог времена. Српски превод Петровићеве дисертације урадио је академик Богољуб Станковић.
Неке од својих најважнијих резултата Петровић је добио већ у докторској дисертацији, стога укратко описујемо тему ове дисертације и њен главни резултат. У тези Петровић изучава класу нелинеарних диференцијалних једначина првог реда, као и нелинеарних диференцијалних једначина другог реда; ове друге су познате под називом једначине Пенлевеа. Ова проблематика у то време била је доста популарна. Крајем XIX века, највећа имена француске и светске математике Пикар, Пенлеве и Фукс проучавали су нелинеарне једначине другог реда са непокретним тачкама гранања. У том контексту Пенлеве, касније Фукс и још касније (1910) Гамбијер описали су поткласу ових једначина које имају облик
$y“=F(x,y,y’)$
где је $F$ количник два полинома по $y$ и $y’$ са холоморфним функцијама као коефицијентима. Пенлеве је пронашао педесет општих форми које имају непокретне тачке гранања које је, уз помоћ Фукса и Гамбијера, свео на шест есенцијално нових једначина. То су оне које се не могу решавати помоћу познатих специјалних функција као што су елиптичке функције, затим које се не могу решавати преко линеарних једначина а и не могу се трансформисати једне у друге. Тих шест једначина носе назив једначине Пенлевеа. Ових шест генеричких случајева данас имају велики значај у многим областима анализе, алгебре и геометрије, али и у применама као што су статистичка механика, физика плазме, теорија нелинеарних таласа, теорија квантне гравитације, квантна теорија поља, теорија релативности и нелинеарна оптика. Пенлев је своје прве резултате добио у радовима који су објављени 1887. и 1895. године. На овој проблематици радили су и највећи међу њима, Поенкаре и Пикар. Ову чињеницу посебно истичемо с обзиром на то да је Михаило Петровић одбранио своју докторску дисертацију управо пред комисијом у којој су били Пикар и Пенлев.


Слика 2. и 3. Корице и прва страна из Петровићеве докторске дисртације.
Докторска дисертација Михаила Петровића је посвећена непокретности нула, полова и есенцијалних сингуларитета решења алгебарских диференцијалних једначина првог и другог реда. Сходно дефиницији, сингуларитете решења чине њени полови, есенцијални сингуларитети, коначне и логаритамске тачке гранања, док се покретност дефинише као својство према којем се нуле и сингуларитети непрекидно мењају са мењањем почетних услова за дату једначину. Другим речима, својство покретности утврђује да ли се ради о „добро“ постављеном проблему, за разлику од „лоше“ постављеног који често и нема решење ако се почетни услови промене. Михаило Петровић је изучавао проблеме за које решења једначина имају сингуларитете независне од промене почетних услова.
У првом делу докторске дисертације Петровић анализира нелинеарне једначине првог реда у којима се појављују производи степена непознате функције y њеног извода $y’$, као и холоморфних функција по независној промељивој $x$:
\begin{eqnarray*}
F(x,y,y’) \equiv \sum_{i=1}^{s} \phi_{i}(x)y^{m_{i}}(y’)^{n_{i}}=0.
\end{eqnarray*}
У исказу главног резултата у тези важно место има полигон $P$ који Петровић конструише на следећи начин. Полигон $P$ има $s$ теменa $(M_{i},N_{i})$, $N_{i} =n_{i}$, $M_{i} =m_{i} + n_{i}$ , $i= 1, \ldots , s$, која су уређена по одређеним правилима, док са $(M_{\alpha},N_{\alpha})$, односно $(M_{\beta},N_{\beta})$, означава најудаљеније, односно најближе теме оси ΟΝ, док са λ означава коефицијенте правца страна полигона. Његов резултат тада гласи: Полови и есенцијални сингуларитети општег решења једначине првог реда $F(x,y,y’)=0$ не мењају се са интеграционом константом ако, и само ако, придружен полигон нема ниједно теме десно од највише издигнутог темена полигона. За постојање покретне нуле реда $\lambda$ потребно је и довољно да полигон има страницу са нагибом $\lambda$ а има покретан пол реда $\lambda$ ако, и само ако, полигон има страницу са нагибом $-\lambda$.
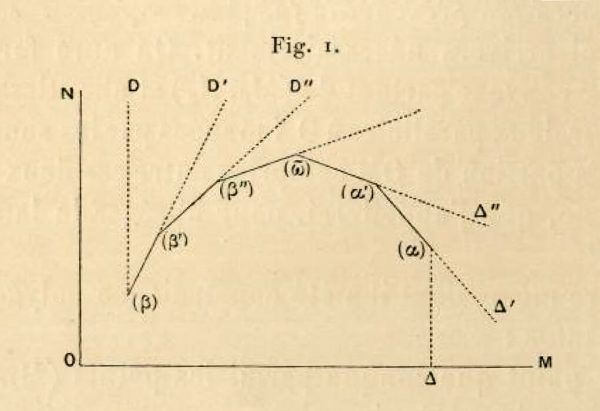
Слика 4. Полигон P, цртеж из Петровићеве дисертације.
Према подацима које је анализирао историчар др Драган Трифуновић, Петровић је објавио 393 публикације од којих су 328 математички рукописи из дванаест области, и то у најпознатијим часописима тог и данашњег времена. У Comptes Rendus, у којем се по мишљењу француских математичара штампају најквалитетнији радови, Михаило Петровић је објавио тридесет рукописа. Такође је публиковао у Acta mathematica, Mathematische Annalen (два рада), Bulletin de la Sociètè mathèematique de France (четрнаест радова), American Journal of mathematics (три рада), као и у многим другим швајцарским, немачким, чешким и пољским часописима. С обзиром на број објављених рукописа у водећим међународним часописима, Петровић је и даље један од наших најпродуктивнијих математичара.
Први Петровићев рукопис наговестио је проблематику у докторској дисертацији, а радови који су потом уследили надовезују се на резултате из дисертације. Независност сингуларитета, нула, екстрема или неких других својстава општег решења од константи у свим тим радовима доминира као јасна одредница Петровићевог научног рада. Ово својство је суштинска, конститутивна карактеристика модела којег изучава, односно једначине која описује модел. Када описује резидуум функције, или проучава тзв. биномне једначине првог реда, асимптотику решења, или када пише о „једној класи диференцијалних једначина другог реда“ или о природи решења, да парафразирамо наслове неких од радова, унутрашњи структурални однос зависне и независне променљиве дат самом једначином јесте циљ његових проучавања. Велики стваралачки потенцијал у научном раду који је показао у докторској дисертацији види се такође у радовима писаним и публикованим у периоду Првог светског рата када их Пикар, Апел и Адамар приказују у Контрандију. За време Првог светског рата боравио је у Швајцарској где је радио као шифрант у српској војној команди. И поред ове обавезе, имао је довољно енергије да се такође бави озбиљним математичким проблемима.
Квалитативна анализа решења диференцијалних једначина, без решавања саме једначине, као и решавање одређених класа једначина представљају значајни део математичког опуса Михаила Петровића. С временом, са све дужим боравком у Србији а краћим боравцима на Сорбони, уочавамо да је Петровић нове идеје надограђивао на оне из докторске дисертације, као и на изузетно добро познавање теорије аналитичких функција. У већини првих радова са краја XIX и почетка XX века, он углавном разрађује идеје до којих је дошао током боравка и научног рада у Француској. Наравно, предности боравка у Француској биле су велике и многобројне. Тако, тамо је Петровићу била доступна тада најновија и најважнија литература, а поред свега имао је непосредне контакте са највећим математичарима тог доба са којима је могао размењивати своје идеје и резултате и дискутовати о њима. Како је у тези посебно изучавао решења једначине $y’= R(t,y)$ са особином Пенлевеа, посебно се бавио разним формама Рикатијеве једначине
$z'(t) = 2α(t)z(t) + b(t) -c(t)z^2(t),$
која може бити решена интеграцијама и помоћу познатих специјалних функција. Фукс је показао да се једначине првог реда, које је проучавао и Петровић, а које имају решења се непокретним тачкама гранања, своде на Рикатијеву једначину општег типа. Неколико теза његових докторских студената је користило ову чињеницу као полазну. Петровићеви математички доприноси нису се исцрпљивали нити почивали само на већ поменутим идејама и методама. Тако су, не само њему већ и његовим докторским студентима, теореме о упоређивању решења једначина у односу на поређење коефицијената или десних страна једначина, тзв. теореме Штурмовог типа, биле честа инспирација. Његово истраживање често су красиле једноставне али фине математичке досетке помоћу којих је успевао да добије резултате општег карактера за разне класе линеарних и нелинеарних једначина. Асимптотика решења, углавном нелинеарних једначина типа Рикатија, такође је имала важно место у њговој анализи једначина.
Петровићеви радови припадају првенствено областима анализе: диференцијалним једначинама, комплексној и реалној анализи. У нумеричкој математици дао је значајан прилог, монографију Анализа бројчаних размака. Интервалнa нумеричкa анализa je овом монографијом добила изузетан подстицај. На самом почетку XX века, у аналитичкој теорији функција проучавао је функције чији Тејлорови редови немају нула у одговарајућем кругу конвергенције. Угледни математичари Ландау, Харди Фејер, Монтел, Поља били су заинтересовани и проучавали су овај његов рад, док је немачки математичар Јенч ове резултате даље разрадио у докторској дисертацији. Позната Петровићева неједнакост је резултат повезан са конвексним функцијама. Она је била инспирација неколицини његових ученика да се баве неједнакостима и постигну значајне успехе у тој области. Монографија – уџбеник Елиптичке функције и данас је радо читано дело у области трансцедентних функција. Од времена Михаила Петровића немамо бољи уџбеник у овој важној области анализе. На овоме се не завршава спектар Петровићевих математичких интересовања. На пример, у више радова бавио се одређивањем – рачунањем одређених интеграла преко редова.
Петровић такође има радова у области алгебарских једначина. У тој области је посебно интересантан рад из геометрије нула полинома, који је такође проучавала наведена група чувених математичара Ландауа, Хардија Фејера, Монтела, Поља. Одредио је прстен у коме алгебарска једначина има бар један корен, не користећи Рушеове теореме. Његов рад из 1899. године, објављен у Контрандију, први је рад који одређује број нула садржаних у датом кругу.
Читајући научне студије Михаила Петровића из периода после Великог рата, уочава се постепени пад квалитета. Радови су мање дубоки, али и даље носе одређене идеје можда већ виђене, али ипак у новом духу. За разлику од данашњег стила, Михаило Петровић излаже резултате од посебних ка општим. Имао је лакоћу писања, па је у својим рукописима, као у кавој причи, најпре наводио једноставне закључке које је постепено уопштавао да би их на крају у потпуности објаснио и трансформисао у тврђења. Овакав приступ омогућавао је читаоцу да врло лако прати излагање и разуме циљеве списа од самог почетка.




Слика 5. Докторанди професора Петровића: Тадија Пејовић, Константин Орлов, Драгољуб Марковић и Јован Карамата.
У научном раду треба истаћи и монографију Математички спектри (која није у вези са данас веома развијеном спектралном теоријом оператора) у којој Петровић, у аналогији са светлосним спектрима, развија теорију математичких спектара. Ово доста обимно и оригинално Петровићево дело не припада анализи, већ је ближе теорији бројева и криптографији, дисциплинама за које се такође занимао. Основна идеја ове његове теорије је да се бесконачни низови података кодирају бесконачним децималним развојима реалних бројева, а затим да се математичке операције над подацима преведу у одређене нумеричке или комбинаторне поступке над бројевима – њиховим кодовима. Петровића су посебно занимала понављања у групама цифара и у томе је видео аналогију са физичким спектрима. Мада је написао књигу на француском, имао похвале одређених француских математичара и одржао један семестар предавања на Сорбони, ова теорија ипак није значајније заживела. Један занимљив поглед даје француски математичар Бул који у приказу овог дела на једном месту каже „да су таква поређења ризична и да као шаре код најсјајније дуге могу бити заводљива али и варљива“. С друге стране, савремени дигитални рачунари, већ као што им име каже, не раде ништа друго до елементарне аритметичке и основне комбинаторне операције над бинарним кодовима низова података, мада семантика нашег проблема над подацима и решавајућег алгоритма лежи на неком сасвим другом месту. Отуда можемо сматрати да се ово Петровићево дело једноставно појавило пре времена. Овој области се посветио касније у дисертацији његов студент професор Константин Орлов, један од најистакнутијих следбеника професора Петровића у области диференцијалних једначина и нумеричке анализе.
Прилози који се односе на примену диференцијалних једначина датих у његовом чувеном делу Феноменологија, као и у низу радова описа модела у физици и хемији дати су у посебним чланцима у Каталогу.

Слика 6. Михаило Петровић Алас у позним годинама.
Михаило Петровић је припадао генерацији највећих математичара у областима аналитичке теорије диференцијалних једначина, која је тада била на врхунцу развоја и у том контексту треба сагледати изузетно висок научни ниво који су имала његова истраживања. Већина његових докторанада су у својим тезама обрађивали теме повезане са нелинеарним обичним диференцијалним једначинама, углавном Рикатијевог типа, или са квалитативном анализом одређених класа једначина. Ипак, нема пуно њихових радова, у теоријском смислу, у којима су они отишли даље од оног што је већ урадио Михаило Петровић. Крајем XIX и почетком XX века, насупрот методама класичне теорије једначина појављују се нове апстрактне теорије засноване на суштински новим приступима у анализи у креирању математичких модела. Следбеници Михаила Петровића, а касније и њихови ученици у областима диференцијалних једначина, изгледа да су мање пратили развој математичке физике или других грана математике у којима су резултати Пенлевеа и Пикара остали доминантни. Недовољно је праћена теорија парцијалних диференцијалних једначина, која се изузетно брзо развијала и у теоријском смислу и у смислу примена у готово свим природним и техничким наукама. Ни сам Петровић није пратио нове правце развоја теорије парцијалних диференцијалних једначина са потпуно новим методама произашлим из тада модерних области, скуповне и алгебарске топологије, геометрије и алгебре, а посебно из функционалне анализе. Резултати Хилберта, Лебега, Дирака, Банаха, Собољева и многих других донели су потпуно нове погледе на математичка истраживања и њихову везу са другим научним областима. Посебно је овај напредак и развој математике у свету био интензиван после Првог светског рата. Свакако да треба узети у обзир да је тада Михаило Петровић већ имао око педесет година и да је дуго био ван научних токова због компликованих прилика у Србији после Великог рата.
Михаило Петровић је био прилично усамљен као стваралац. Све радове, сем једног са Караматом, написао је сам, а тај рад је интересантан због тога што исправља једну грешку Поенкареа. Разлог можемо потражити у његовој изразитој индивидуалности. Није увек до краја разрађивао идеје, тако да су други, имајући у виду његове резултате и идеје, написали дубље радове који су између осталог више цитирани. Међу колегама није било оних који би га посебно истицали већ и због тога што су сви, овде мислим на математичаре у Француској, пре свега тежили личном престижу, без обзира на Петровићеву сјајну природу и склоност пријатељствима. С обзиром на то да је у то време код нас било мало математичара и да је Петровић био први наш математичар који се бавио овим проблемима, није ни могао имати значајнију математичку подршку у Србији, посебно у периоду између два рата.

Слика 7. Потврда о чланству у Чехословачком математичком друштву.
Михаило Петровић није био много заинтересован да буде цитиран, а није га ни много интересовало да ли га у математици неко прати или не. С друге стране, математичари с краја XIX и почетка XX века нису имали пуно могућности за цитирање, а нису имали ни навику таквог међусобног опхођења у науци. У тези Михаила Петровића, као и у његовим радовима цитирање резултата других математичара није у форми која је данас општеприхваћена. Цитираност у области у којој је Петровић највише радио давана је најчешће кроз навођење резултата који су приписивани Пикару, Фуксу а свакако највише Пенлеву. И сам Михаило Петровић у тези има врло оскудну литературу, свега осам референци. Радови Михаила Петровића су цитирани у времену које је блиско периоду када их је писао, али мислимо да је то било недовољно. Радови у Acta Mathematica, Математичким аналима и низу других часописа, посвећени проблематици из докторске дисертације, као и већина других радова били су цитирани крајем XIX и почетком XX века. Резултати првог Петровићевог рада објављеног у Контрандију комплетно су наведени у чувеној, тада најцењенијој Пикаровој монографији, док су резултати докторске дисертације цитирани у Енциклопедији математике. Ипак, у вртлогу догађаја балканских ратова и Првог светског рата, Михаило Петровић полако бива све мање присутан у Француској, што је значило и у светским круговима у којима се стварала и развијала нова наука.
Михаило Петровић је излагао своје радове на читавом низу значајних међународних конгреса математике у Паризу, Риму, Кембриџу, Торонту и конференција научних федерација Француске (десетак пута), Румуније, Италије, словенских земаља и земаља са Балкана.
Петровић је био цењен и уважаван као научник не само у Србији већ и у целој Европи. Био је члан Југословенске академије знаности и умјетности, Чешке краљевске академије, Пољске академије наука у Кракову, Академије наука у Варшави, Румунске академије наука и читавог низа матeматичких друштава у Паризу, Палерму, Букурешту, Лајпцигу, Прагу, Лавову, а у Паризу је био члан неколико научних друштава.
Допринос у образовању
У улози коју му је подарио стицај околности, академик Петровић је од прворазредног значаја за развој универзитетске наставе математике у Србији. У периоду до Првог светског рата, као и између два светска рата професор Петровић је готово сам развијао образовни универзитетски математички систем Србије. Редовни је професор математике од 1894. на Великој школи на Филозофском факултету, а од 1905. на Београдском универзитету. Био је једини који је водио математичке докторате на Београдском универзитету, од 1912. до 1941. Није објавио пуно уџбеника, само три, али његова скрипта писана руком су изузетног квалитета и право је задовољство читати их и данас. Држао је 16 различитих курсева: из анализе и диференцијалних једначина 10 курсева, из алгебре два курса, из нумеричке математике три и посебно курс из феноменологије. Написао је осам скрипата. Био је члан комисије за полагање професорског испита, изасланик министарства на испитима зрелости, председник Главног просветног савета Србије, био је референт за средњошколске уџбенике и имао је и неколико радова посвећених методици.



Слика 8. Наследници у математици професора Петровића: академик Слободан Аљанчић, академик Богољуб Станковић и професор Славиша Прешић.
Михаило Петровић је био строг и принципијелан професор. Записано је да није одржао ниједан јавни говор, што и није неуобичајено међу математичарима. Са Милутином Миланковићем и Антоном Билимовићем 1932. године основао је часопис Publications de l’Institut Mathématique. Резултат великог ангажовања у наставном раду је за многе наше математичаре, математичке наследнике професора Петровића, непознат. Велики број математичара у Србији има као математичког претка професора Михаила Петровића Аласа. Према непотпуним подацима тај број износи око петсто доктора математике у Србији. Поред ученика академика Ђуре Курепе и математичара у Србији који су докторирали у иностранству код разних ментора, као и геометричара који у корену имају професора Данила Бланушу, велики је број нас који имамо блиског математичког претка Михаила Петровића. Наведимо и имена његових ученика прве генерације, професора Мирослава Берића, Симе Марковића, Драгољуба Митриновића, Константина Орлова, Тадије Пејовића, Данила Михњевића, Милоша Радојчића. Академици из те прве генерације су Радивој Кашанин и Јован Карамата, у другој генерацији то су академици Војислав Авакумовић, Миодрг Томић, Слободан Аљанчић, Војислав Марић, Милосав Марјановић, Драгош Цветковић, Градимир Миловановић, а у трећој академици Иван Гутман, дописни члан Миодраг Матељевић и писац овог текста.
Имам велику обавезу да наведем наше изузетно цењене математичаре, потомке академика Петровића који су преминули, професоре Манојла Маровића, Ернеста Стипанића, Татомира Анђелића, Милорада Бертолина, Милице Дајовић и Војина Дајовића, Петра Васића, Славишу Прешића, Миливоја Лазића, Загорку Шнајдер, Светозара Милића, Зорана Ивковића, Јанеза Ушана, Душана Адамовића, Драгољуба Аранђеловића, Владету Вучковића, Богдана Бајшанског, Ранка Бојанића, Татјану Острогорски, Зорана Попстојановића, Љубу Протића, Рада Дацића… Све нас повезује академик Михаило Петровић. Многа имена нису споменута. О њима, као и о онима који су још активни податке можемо наћи у математичкој генеалогији академика Петровића у овом каталогу..
Рад у Академији

Слика 9. Академици Михаило Петровић, Богдан Гаврилоић и Милутин Миланковић.
Како је већ наведено, Михаило Петровић Алас је постао дописни члан Српске краљевске академије 1897. године, а редовни члан 1899. годин. Свечани пријем је обављен 1900. исте године када је и Јован Цвијић постао редовни члан Српске краљевске академије. Академик Петровић је био врло активан у раду Академије. Био је секретар Одељења природних наука, па тако и члан Извршног одбора Академије. Писао је приказе радова математичара који су публиковали радове у Гласу Академије а представљао је и нове кандидате за чланство у Академији. У Гласу Српске краљевске академије објавио је око шездесет радова и тиме значајно допринео угледу Академије. По традицији коју и данас следимо, а то је и традиција Француске академије, радове аутора ван Академије су реферисали чланови. У тим активностима Михаило Петровић је био веома активан посебно због тога што су његови ђаци публиковали велики број својих најважнијих радова управо у Гласу Српске краљевске академије. Промовисао је читав низ акдемика, рецимо Богдана Гавриловића, 1900, Милутина Миланковића, Антона Билиновића и Јована Карамату.
Јован Цвијић, Михаило Петровић и Богдан Гавриловић су 1909. позвали Милутина Миланковића да пређе из Беча на Београдски универзитет, што је он и учинио. Предложили су Миланковића за дописног члана 1920. а за редовног 1925. године. Када је умро Јован Цвијић, 1927. године, Петровић је био најозбиљнији кандидат за председника Српске краљевске академије, али изабран је Слободан Јовановић.

Слика 10. Зграда Академије, подигнута 1924. по плановима Драгутина Ђорђевића и Андре Стевановића у стилу академизма са елементима сецесије.
Јован Карамата је промовисан за члана Академије 1939. Свом учитељу Михаилу Петровићу је много помогао у сређивању научних публикација. Захваљујући томе, а и великој жељи Михаила Петровића да среди своје папире и своју заоставштину, данас имамо обиље података о његовом животу и раду.